中間値の定理とは
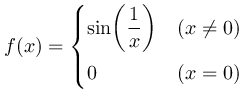
言葉で書くとものすごく難しいことを言ってそうですが、実際はそうではありません。
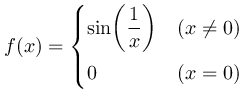

言葉で書くとものすごく難しいことを言ってそうですが、実際はそうではありません。
気をつけて欲しいのはあくまで 決められないことがあるだけです。 。


いったん広告の時間です。 このとき、グラフは次のようになります。
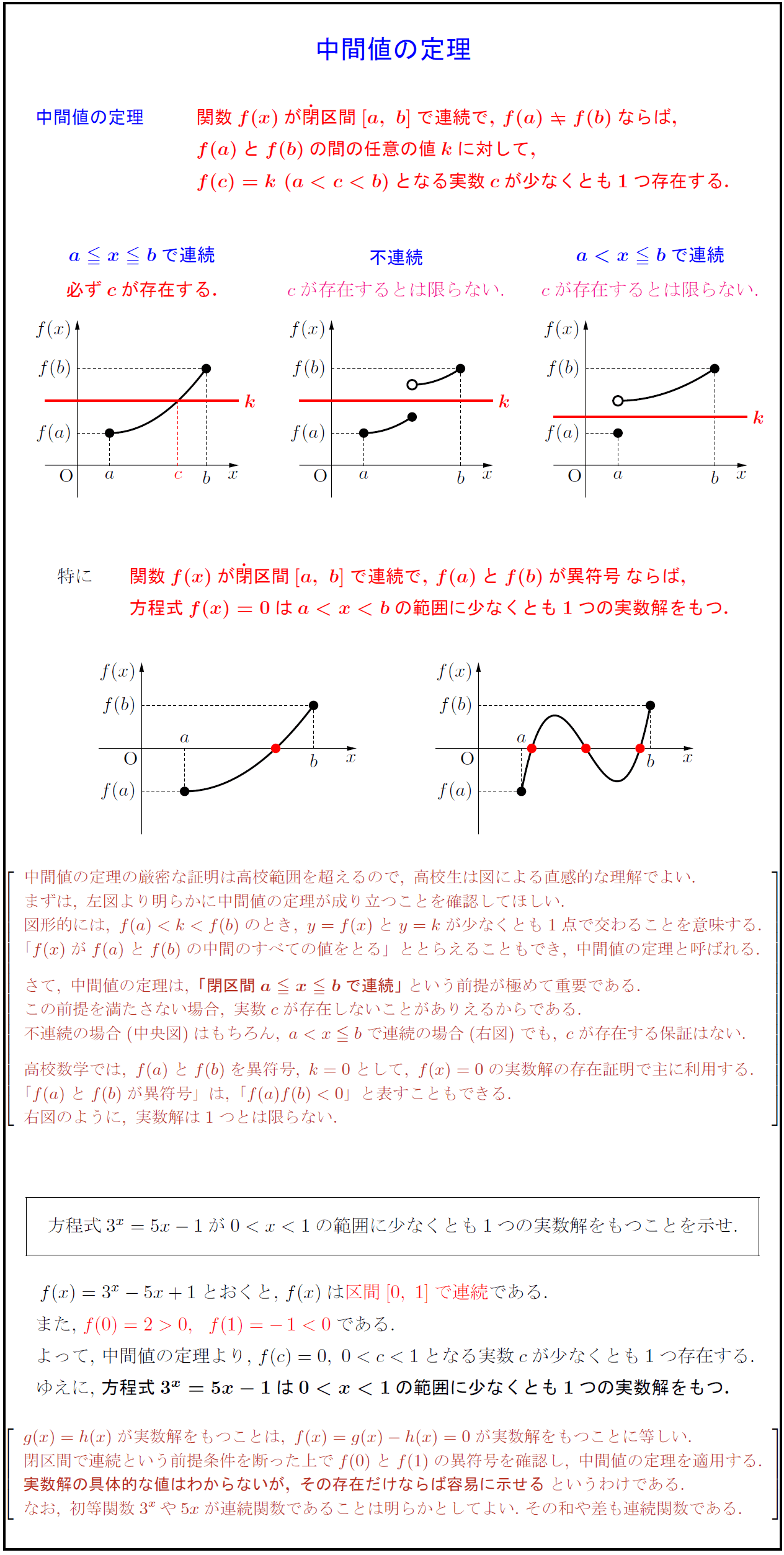
の連続像は連結である。 逆にこれのどちらも、もしくはどちらかを満たさなければその関数は「不連続である」 と言うことでした。


一見解決策がなさそうな問題でも中間値の定理を使えば簡単に示すことができましたね。
これがないときは、実数解が存在するかどうはわかりません。
もちろん 定義域もこの区間なので対数関数も連続関数です。
そうなんですよね、確かにこれだけだと当たり前に思うのですが、 これをうまく使うと非常に重要な問題が簡単に解けてしまうのです。
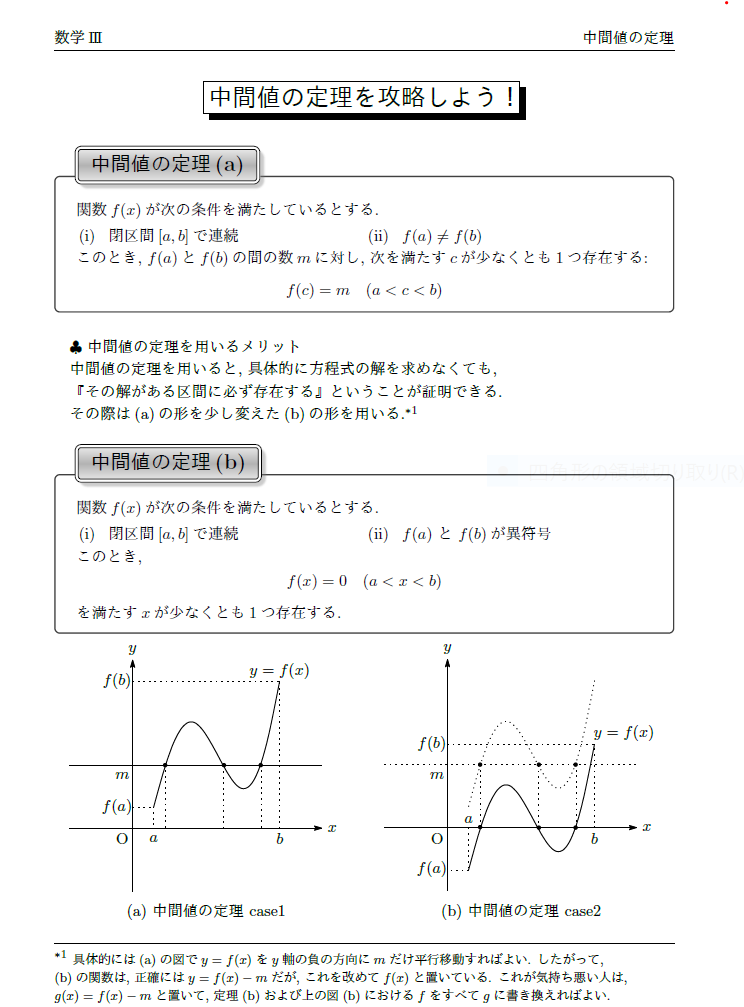
この事実を中間値の定理という。
さて、言葉がわかったところでちょっと練習します。 その区間で連続であれば、つまり「しっかりとつながっていれば」その区間で必ず最大値と最小値があるということです。
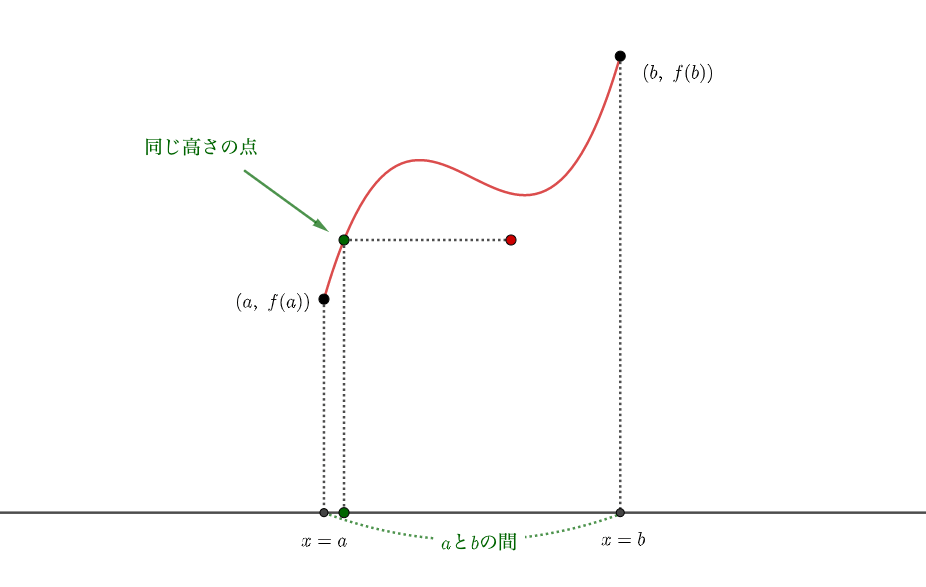
の二つだけである(この事実はここでは認めて話を進めることにする)。 閉区間でつながったグラフであれば最大と最小が必ずあるのは確かにそうっぽいです。 これらは数学の定理の中でも少し変わった内容です。
10そうでないと言っても、 「ある一点」で連続でないだけで、それ以外では連続であることがほとんどです。 しかし、これを満たす実数解が1つは存在する、ということはわかるんですね。


次で実際の例を見てみます。 いろいろグラフをかいて確かめてみましょう。 このことは、「間の値をとる」ということから、 中間値の定理 intermediate value theorem と呼ばれています。
実は数学の、特に関数の分野では、この「範囲」のことを 「区間」と言い、不等式で書くよりも簡単な記号で書くことにしています。